ブログ名

競技プログラミングやお歌のお話をする高菜です。

トップ > `next_permutation` と同様に列挙できるもの一覧

`next_permutation` と同様に列挙できるもの一覧

1. 置換（permutation）

長さ $N$ の数列 $A$ の置換を列挙します。辞書順で $A$ より大きな最小の置換 $A$ があればそれを求め、なければ報告するアルゴリズムが作れればよいです。

C++ に std::next_permutation がありますね。言わずとしれた C++ ナニコレアルゴリズムライブラリさんのひとつです。なおバージョン 1.70.0 現在、Rust の標準ライブラリにはありません。作りましょう。

説明の簡単のため、$A$ の要素は相異なると仮定しますが、そうでなくとも全く同様です。

  1. 変更のある最も前側のものは、後ろ側から見て初めて単調減少ではなくなるものです。これを $A_i$ と置きます。（もう少し厳密に言うと、$A_i \lt A_{i + 1} \ge A _ {i + 2} \ge \dots$）
  2. $A_i$ は、$A_i$ よりも後ろ側にある $A_i$ よりも大きな最も小さなものです。これを $A_j$ と置き、$A_i$ と $A_j$ をスワップします。
  3. あとは $A _ {i + 1}$ 以降をソートすればよいのですが、現時点で降順になっていることに注意すると、単に reverse すればよいことがわかります。

図解するとこうです。右向きが添え字の増える方向で、上向きが値の増える方向です。

next_permutation

pub fn next_permutation<T: Ord>(a: &mut [T]) -> bool {
    let Some(i) = a.windows(2).rposition(|w| w[0] < w[1]) else { return false };
    let j = a.iter().rposition(|x| x > &a[i]).unwrap();
    a.swap(i, j);
    a[i + 1..].reverse();
    true
}

2. シャッフル（shuffle）

長さ $N$ の数列 $A$ の置換であって、前 $K$ 項、後ろ $N - K$ 項がそれぞれソートされているものを $(K, N - K)$-shuffle と呼びます。これを列挙しましょう。

そのために、いま $A$ が $(K, N - K)$-shuffle であるとして、$A$ より大きな最小の $A$ の $(K, N - K)$-shuffle を計算する方法を考えましょう。記述の簡単のため $A$ の要素は相異なると仮定しますが、そうでない場合も全く同様です。 前 $K$ 項を $L$、後ろ $N - K$ 項を $R$ と置きます。

  1. すると $L$ のうち更新される最小のものは、$R$ の要素の最大値よりも小さいもののうち最大のものです。これを $L_i$ と置きます。（存在しない場合は、next shuffle が存在しません。）
  2. さらに $L _ i$ は $R$ の要素のうち $L_i$ より大きな最小のものと交換されます。これを $R_j$ と置きます。
  3. あとは $L _ {i+1}, \dots,
  4. L _ {K - 1}$ と $R _ {j + 1}, \dots, R _ {N - K - 1}$ を繋げて一つの配列と思い、これを $R _ {j + 1}$ が先頭に来るように回転すれば答えになります。（これ説明難しいです。）

以上の操作は償却 $O ( N - K )$ 時間で実行できます。

ステップ 3 は、要素のコピーができるのでしたら、キューなどを用いて実装してもよいです。 コピーをしたくない、もしくは O(1) extra memory で行いたいということでしたら、標準ライブラリの swap_slice と rotate_{left,right} を用いるとよいです。

next_combination

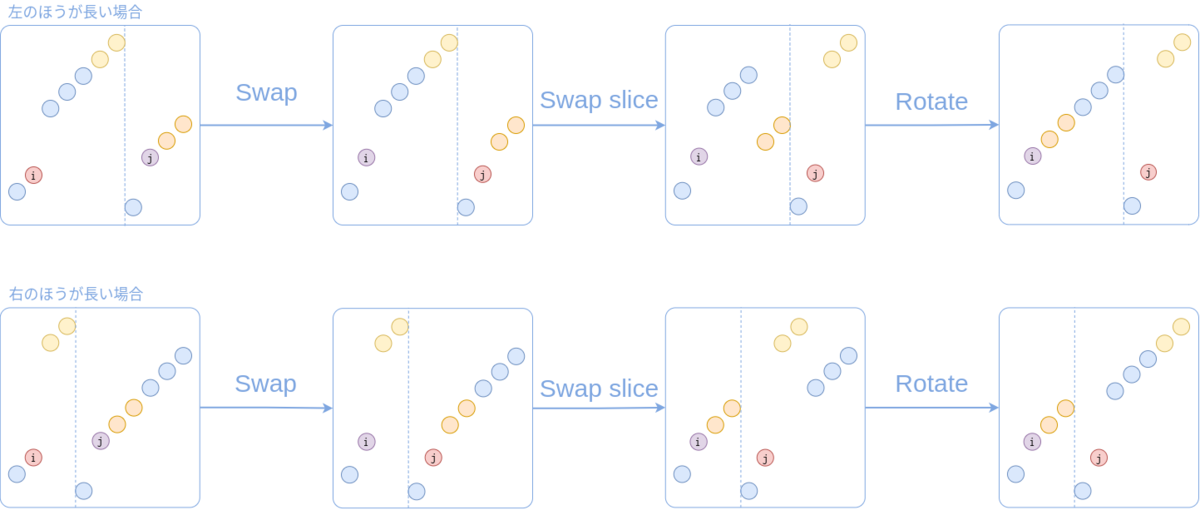
pub fn next_shuffle<T: Ord>(a: &mut [T], k: usize) -> bool {
    let n = a.len();
    if n == k {
        return false;
    }
    let (left, right) = a.split_at_mut(k);
    let Some(mut i) = left.iter().rposition(|x| x < right.last().unwrap()) else {
        return false;
    };
    let mut j = right.iter().position(|x| &left[i] < x).unwrap();
    std::mem::swap(&mut left[i], &mut right[j]);
    i += 1;
    j += 1;
    let swap_len = (k - i).min(n - k - j);
    left[k - swap_len..].swap_with_slice(&mut right[j..j + swap_len]);
    left[i..].rotate_left(k.saturating_sub(i + swap_len));
    right[j..].rotate_right((n - k).saturating_sub(j + swap_len));
    true
}

ABC 328 E - Modulo MST ユーザー解説

3 ascending $(2, 2, ..., 2)$-shuffle

$1, \dots, 2N$ の置換 $A$ が $(2, 2, ..., 2)$-shuffle であるとは　$A _ { 2 i - 1 } \le A _ { 2 i } \ ( 1 \le i \le N )$ を満たすことを言います。このようなもののうち ascending、すなわち $A _ 1 \le A_3 \le A_5 \le \dots \le A_{2N - 1}$ であるものを列挙しましょう。

$A$ が ascending $(2, 2, ..., 2)$-shuffle として、辞書順で $A$ より大きな最も小さな ascending $(2, 2, ..., 2)$-shuffle を計算しましょう。これは後ろから順に見て、増やせる所があれば $1$ 増やし、残りを昇順に埋めていけばよいです。

fn next_pairing(p: &mut [usize]) -> bool {
    let n = p.len();
    let mut used = 0_u32;
    for i in (0..n).rev() {
        used |= 1 << p[i];
        if i % 2 == 1 && p[i] + 1 < used.ilog2() as usize {
            p[i] = (used >> (p[i] + 1)).trailing_zeros() as usize + p[i] + 1;
            used ^= 1 << p[i];
            for i in i + 1..n {
                p[i] = used.trailing_zeros() as usize;
                used ^= 1 << p[i];
            }
            return true;
        }
    }
    false
}

[ABC 236 D - Dance ユーザー解説[(https://atcoder.jp/contests/abc236/editorial/3316)

4. 自然数の分割

$A$ が自然数 $N$ の分割であるとして、$A$ よりも辞書順で大きな辞書順最小の $N$ の分割を求めましょう。

  1. 後ろから見て最初に増加する箇所を探し、$A_i$ とおきます。（もう少し厳密にいうと $A_i \gt A _ {i + 1} = A _ {i + 2} = \dots$、ただし $A_i$ は末尾ではありません。）
  2. $A_i$ を $1$ 増やし、あまりをすべて $1$ にします。

逆順に走査することもできます。

pub fn next_partition(a: &mut Vec<usize>) -> bool {
    let Some(mut sum) = a.pop() else { return false };
    if a.is_empty() {
        return false;
    }
    while let Some(x) = a.pop() {
        sum += x;
        if a.last().map_or(true, |&last| last > x) {
            a.push(x + 1);
            a.extend(std::iter::repeat(1).take(sum - x - 1));
            break;
        }
    }
    true
}
pub fn prev_partition(a: &mut Vec<usize>) -> bool {
    let Some(i) = a.iter().rposition(|&x| x != 1) else { return false };
    let max = a[i] - 1;
    let mut sum = a.split_off(i).into_iter().sum::<usize>();
    while sum >= max {
        a.push(max);
        sum -= max;
    }
    if sum > 0 {
        a.push(sum);
    }
    true
}

ABC 226 F - Score of Permutations ユーザー解説

5. カルテシアン冪

簡単なのでコードのみです。

let mut a = vec![0; n];

loop {
    match a.iter().rposition(|&x| x + 1 != k) {
        None => break,
        Some(i) => {
            a[i] += 1;
            a[i + 1..].iter_mut().for_each(|x| *x = 0);
        }
    }
}

6. next_valid_paren (追記: 2022-01-03；工事中）

TODO: 何をするものかご説明します。

後ろから見て初めて ()) の形になっている箇所を見つけて、i と置きます。

すると、こういう感じのをこういう感じにすればよいので、i と i + 1 をスワップして、i + 2 以降をソートです。

i
())))))))))))))()()()()()()()()
)()))))))))))))()()()()()()()()
)((((((((()))))))))))))))))))))

match s.windows(3).rposition(|v| v == &['(', ')', ')']) {
    None => break,
    Some(i) => {
        s.swap(i, i + 1);
        s[i + 2..].sort();
    }
};

こういうやり方もありますが、どちらが速いのかはわかりません。

loop {
    match s.rchunks(2).position(|v| v[0] == ')') {
        None => break,
        Some(count) => {
            let i = s[..n - 2 * count].iter().rposition(|&c| c == '(').unwrap();
            s.swap(i, i + 1);
            s[i + 2..i + 2 + count].iter_mut().for_each(|x| *x = '(');
            s[i + 2 + count..].iter_mut().for_each(|x| *x = ')');
        }
    }
}