Splay 木の計算量解析 - ブログ名の続編的な記事です。数年ブログをやっていて、続編が実際に出たのは初めてですね。（あの？）

Link-Cut 木概論

Link-Cut 木は根付き森を管理するデータ構造です。

Link-Cut 木は内部的に、preferred path と呼ばれる節点素なパス被覆をなんらかの形で管理します。Preferred path に含まれる辺を preferred edge、含まれない辺を unpreferred edge*1 と呼び preferred [resp. unpreferred] edge で繋がった子のことを preferred [resp. unpreferred] な子と呼びます。すると任意の節点は高々 $1$ 個の preferred な子を持ちます。

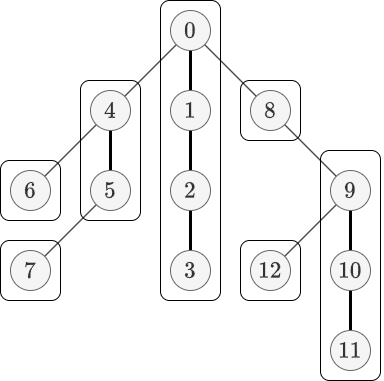
Splay 木ベースの Link-Cut 木は preferred path の節点列を、祖先から子孫に向かって左から右に並んでいるような splay 木で管理します。区別のためにもともとの木を real tree、この splay 木を auxiliary tree*2 と呼ぶことにします。さらに unpreferred edge $(p, c)$ （$p$ が親側、$c$ が子側）に対応して、$c$ を先頭とする preferred path に対応する auxiliary tree の根 $r$ から $c$ へ親ポインタを張ります。ただし $c$ から $r$ には子ポインタを張りません。

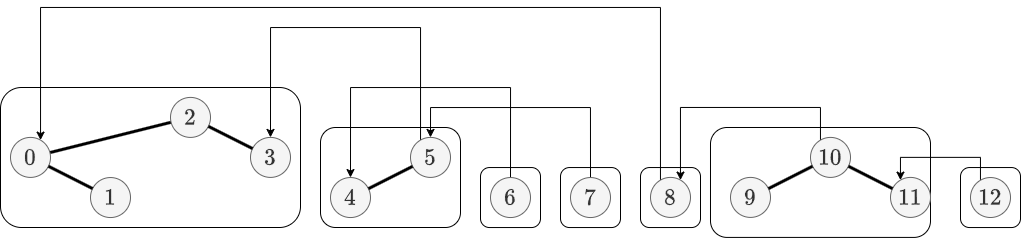
Link-Cut 木の expose は path decomposition を変更することで real tree の根で始まって $x$ で終わる path $P$ を preferred にする操作です。具体的には $P$ が preferred path になるのに加えて、もともと path decomposition に入っていた各 path $Q$ に対してこれが $P$ に含まれるならば削除し、そうではなく $P$ と共有点を持つならば共有部分を除きます。

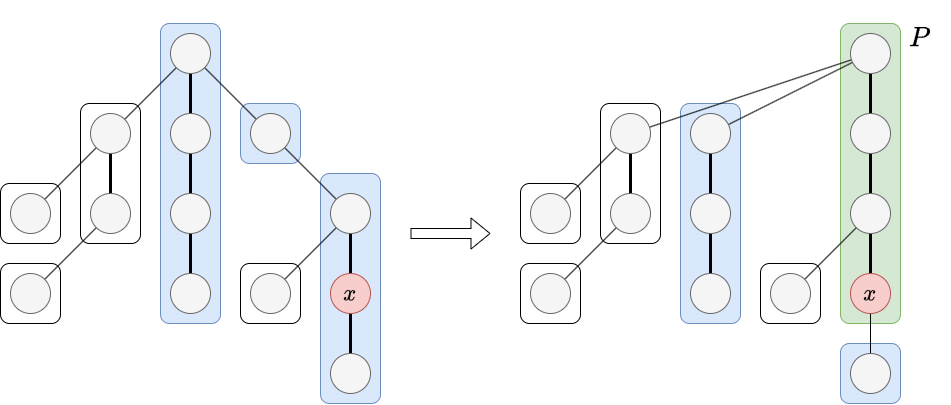
Splay 木ベースの Link-Cut 木の expose は次のようなアルゴリズム*3です。このアルゴリズムが上に説明した通りに path decomposition を変更することを確認してください。

$y ← \mathtt{null}$
auxliary tree において $x$ を splay
$\mathtt{right}(x) ← y,\ y ← x, \ x ← \mathtt{parent}(x)$
$x = \mathtt{null}$ なら終了、さもなくば第 2 行に戻る

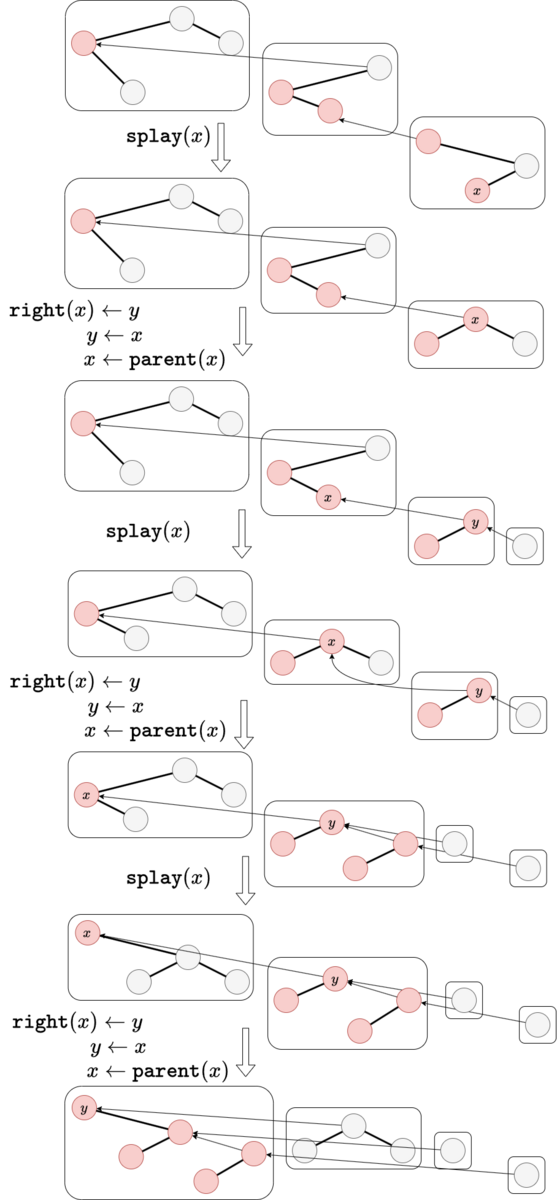
本記事では expose が適切に定義されたポテンシャルで $O(\log(n))$ amortized cost になっていることと、そのほか計算量保証に必要なことを証明していきます。

補題

1 回の expose における preferred edge の選び変えは償却 $O(\log(n))$ 回である

証明

子側のサイズが親側のサイズの半分以上であるような edge のことを heavy edge*4、そうでない edge のことを light edge と呼び、heavy [resp. light] edge で繋がった子のことを heavy [resp. light] な子と呼びます。すると任意の節点は高々 $1$ 個の heavy な子を持ちます。

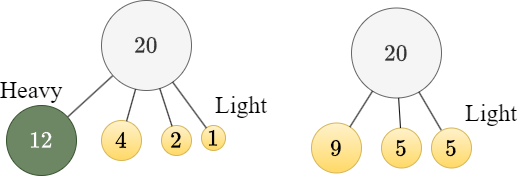
Preferred かつ light である edge の個数 $φ \ ( ∈ [0, n - 1])$ をポテンシャルとして解析します。Preferred edge の選び変えは次の 3 通りに場合分けできます。

light edge から light edge に変更される
heavy edge から light edge に変更される
light edge から heavy edge に変更される

Real tree の根からの任意の path は light edge を高々 $⌊\log(n)⌋$ 個持つので、場合 1, 2 が起きるのは高々 $⌊\log(n)⌋$ 回です。また場合 1, 2, 3 はそれぞれポテンシャル $φ$ を $0, 1, -1$ 増加するので、場合 3 は高々償却 $⌊\log(n)⌋$ 回です。以上より 1 回の expose における preferred edge の付け替えは高々償却 $2⌊\log(n)⌋$ 回です。

Splay 木ベースの Link-Cut 木の計算量解析

ポテンシャル

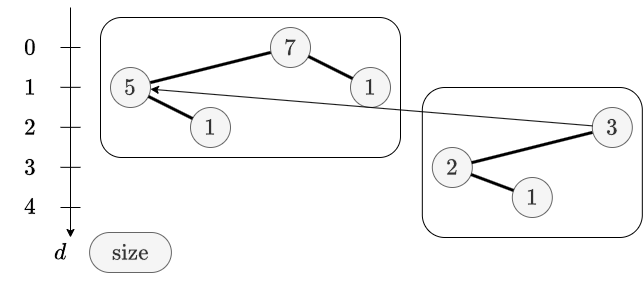
基本的には splay 木の記事中で書いたポテンシャルと同様ですが、auxiliary tree 内での部分木ではなくて一方的に親ポインタが貼られているような関係（unpreferred edge）も親子関係とみなしたときの部分木の節点数を $\mathtt{size}(u)$ とします。先ほどのポテンシャル $φ$ と区別してこのポテンシャルを $Φ$ と表します。

ポテンシャル解析（本題）

Expose 1 回での $Φ$ の増分の合計が $O(\log(n)) - d(x) + O(1)$（ただし $d(x)$ は操作前時点での $x$ の深さ）であることさえ示せれば、splay の実コストが $-d(x)$ と相殺されて全体で償却 $O(\log(n))$ 時間になることがわかります。

これは splay の合間のポインタ貼り替えで $Φ$ が変化していないことや、$x$ への再代入も状況を悪化させない（これにより $\mathrm{rank}(x)$ が増加するものの最後に $\log(n)$ で抑えるときに吸収される）ことに注意しておけばあとは増分を足していけば証明できます。本質的なところはすべて splay 木の記事で解説済みですが、それを十分に理解していない場合は難しく感じると思います。気づきづらいですが、案に最初の補題もここで使っていることにも注意してください。

expose 以外の操作の償却計算量

これもよくある誤解なのですが、実コストが定数だからといって償却コストも定数であるとは限りません。たとえば巨大なスプレー木の真下に巨大なスプレー木を定数時間でくっつけたり場合は、これにより $Φ$ が爆上がりする可能性があります。しかし逆に償却コストの増分が実コストの定数倍で抑えられる（負の場合はいくら大きくてもOK）場合は償却コストも実コストの定数倍になります。

Link-Cut 木の Link で辺 $(p, c)$ を追加するときには、$p$ を expose & splay、$c$ を splay したうえで、$c$ を $p$ の右の子にします。ここで注意すべきなのが最後のポインタ操作です。ここで $Φ$ が爆上がりしていたら元も子もないわけですが、嬉しいことにランクが増えるのは $c$ だけなので、無事 log で抑えられるわけですね。

Link-Cut 木の Cut で辺 $(p, c)$ を削除するときには $c$ を expose したうえで、$c$ の左の子を切り離すわけですが、これについても同様の議論が通ります。さらに evert は木の構造を変更しないので当然ポテンシャルは不変なのでよいです。

参考文献

*1:HL 分解の類推で preferred edge が heavy edge、unpreferred edge が light edge と呼ばれてしまうことがある気がしますが、misleading なのでこの記事ではそうは呼ばないことにします。

*2:いわゆる競プロ方言の auxiliary tree（参考：指定された頂点たちの最小共通祖先関係を保って木を圧縮してできる補助的な木 | Kyopro Encyclopedia of Algorithms）とは全然違うので注意です。

*3:本質的には違いはありませんが、本記事では議論の簡略化のためによくある実装（Link-Cut 木 - ei1333の日記など）とは変えている点が多いことに注意です。

*4:HL 分解のよくある実装（参考：Easiest HLD with subtree queries - Codeforces）では、実装を簡単にする都合上葉でない任意の節点に対してサイズ最大の子を一つ選んで heavy と呼んでいると思います。それとは少し定義が違いますが、今回の議論には影響がありません。